Create a free profile to get unlimited access to exclusive videos, sweepstakes, and more!
Where is the Sun located in the Milky Way?
I get email. Most of the time it's people asking a question or two that are Google-able (hint hint), and sometimes it's a question I have to dig around a bit to answer. I like those, because it means I Get to Learn a Thing.
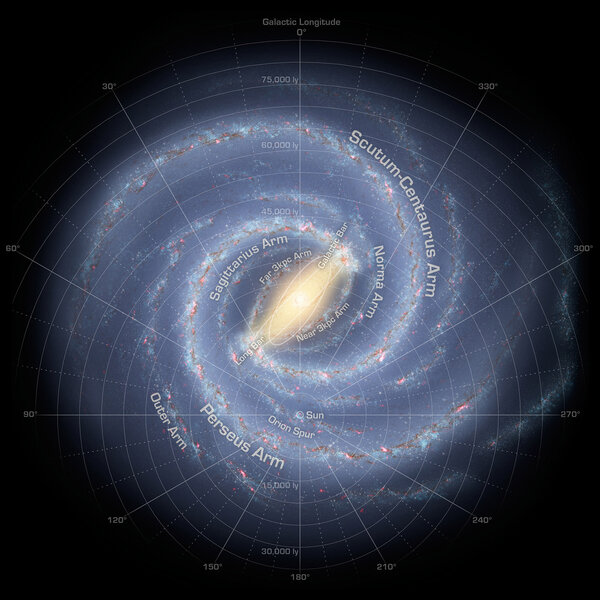
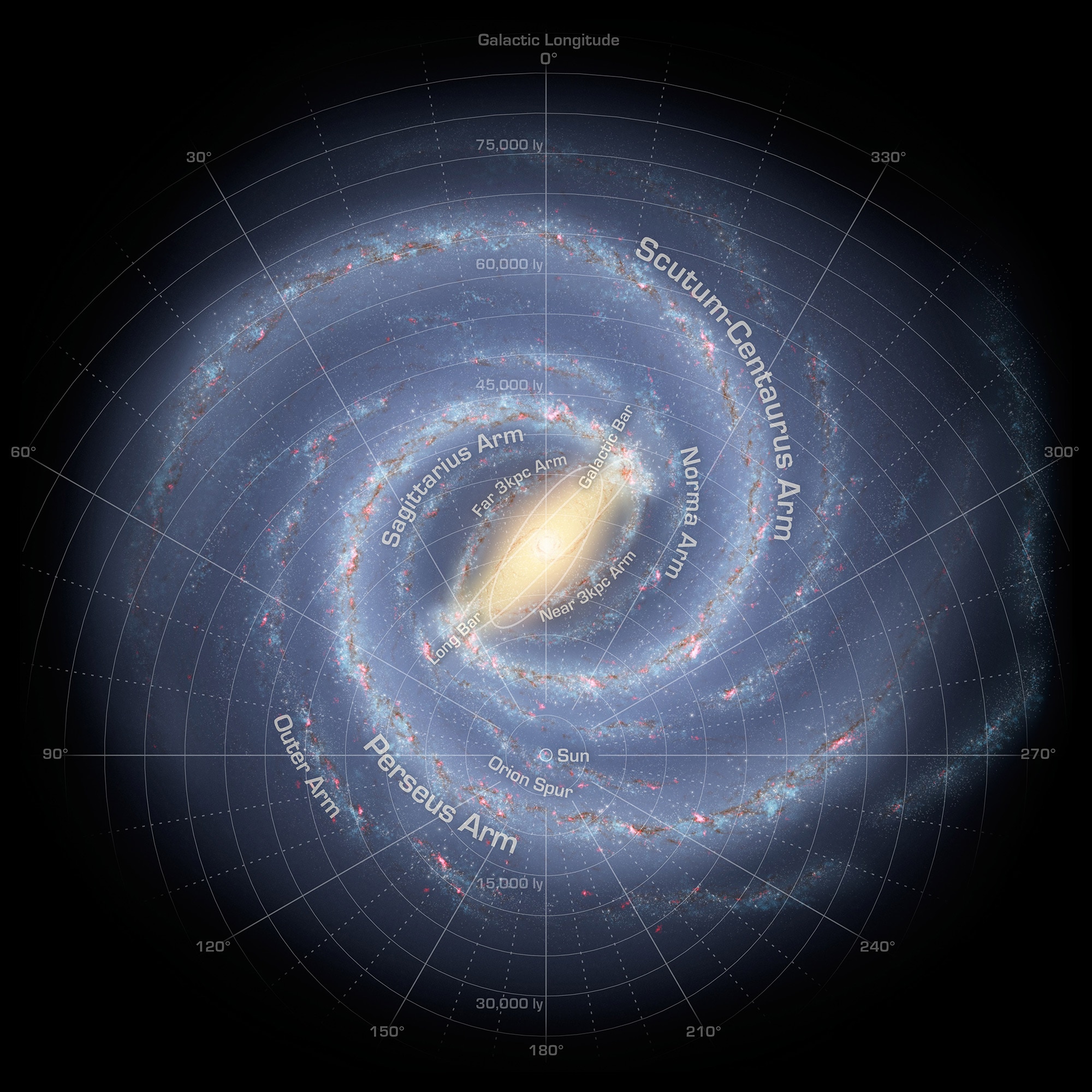
In this case, Bad Reader Joshua Brown it was about the Sun's location in the galaxy. Not how far we are from the center, which we know pretty well now (about 26,700 light years), but how far we are from the midplane of the galaxy. Our Milky Way galaxy is a flat disk 100,000 light years or so across, but it's also about 2,000 light years thick. The actual thickness is hard to define, since the stars kinda fade away as you go up (or down) from the disk, like the Earth's atmosphere thins out as you increase altitude. Also, how thick it is depends on what you measure!
There are actually two disks to the galaxy: a thick disk and a thin disk, with the thin disk right in the middle of the thick one. Imagine the galaxy is a two-layer cake with frosting in between the layers. The frosting is the thin disk, and the cake sponge is the thick one. If the two sponge layers are exactly the same height, then the galactic midplane would slice horizontally exactly through the center of the frosting layer between them. To give you a sense of scale, if the cake is 10 cm high (the top-to-bottom thickness of the thick disk), then to scale with the Milky Way the cake itself would be a circle 5 meters in diameter! That's a very wide, flat cake. The frosting layer in the middle representing the thin disk would be about 4 cm thick, which is a thick frosting layer!).
Also, to this scale, the Sun would be 1.3 meters out from the center, roughly halfway from the center to the edge.
But where is it vertically in the cake? Right in the center of that frosting layer, or off by a bit up or down?
That number has been hard to determine. But in 2016, a couple of astronomers looked into figuring out the galaxy's orientation in space. If it's a flat disk, then the axis of that disk points to a certain spot in the sky. Their goal was to find that spot, but as a by-product they also got a measurement of the Sun's displacement from the midplane. Their result is that we're about 55 light years north of that plane (where "north" is toward galactic north, which is in the constellation of Coma Berenices). Their estimate has a large uncertainty, though, of about 16 light years, but even with that we're certainly north of the midplane.
They measured this by actually measuring the direction to the north galactic pole! They used a bunch of different "tracers" for the disk, objects or groups of objects that trace out the shape of the Milky Way's disk. They then look at the distribution of these objects across the disk, letting that define the plane of the galaxy itself. Once they have that, they can then apply some geometry to find the pole of that plane (think of it as the direction that plane is facing).
They do this two ways: One is "unconstrained," where they just use those tracers to get the geometry. The other way is "constrained," where they force the center of the galaxy to be the location of our central supermassive black hole, Sgr A*. These two methods yield slightly different answers, which they attribute to the Sun not being exactly in the middle of the plane of the disk. When they account for that, they get the 55 light year number.
Coooool. Incidentally, the Sun orbits the center of the galaxy (called the galactic year and sometimes the cosmic year) every couple of hundred million Earth years, but as it does so it bobs up and down with respect to the disk! When it's above the disk midplane, the gravity of the billions of combined stars pulls it down, so it drops back down, passes through the midplane, then drops to a some dozens of light years below the disk, which then pulls it up, and the process repeats. Right now we're still on our way up. The cycle takes about 60 or so million years to complete once.
So, there you go! I knew we weren't in the midplane exactly, but I didn't know by how much we were off, or how that was measured. Now I do. Hopefully now you do too.
My thanks to Joshua Samuel Brown (@josambro on Twitter) for asking the question in the first place!
Correction (Oct. 2, 2019): Getting the thicknesses of the thin and thick disks is a little tricky; the numbers I originally used were too small. The Swinburne Astronomy online course lists them as having scale heights of 400 and 1,000 light years, respectively, which sound about right to me. "Scale heights" are a whole can of worms to open here, but if you have something that gets thinner or less dense with height (like the Earth's atmosphere), the scale height is where its density drops by a factor of 1/e, where e is the base of the natural logarithm, about 2.7. So yeah it's a bit complicated. So the cake is an analogy, but it's solid, so it doesn't work terribly well when you dig intot he details (which is true for all analogies). The point: The thick disk is thicker than the thin disk, and the cake is really wide compared to both!